Trong bài 4 của loạt bài thống kê cho khoa học dữ liệu, chúng ta cùng ôn tập lại về về xác suất và trong bài 3 chúng ta đã tìm hiểu về phân bố ngẫu nhiên hay là phân bố Gaussian cũng như độ phân tán. Trong bài này, hãy cùng tìm hiểu về những khái niệm thống kê vô cùng quan trọng khác, đó là đồng phương sai (covariance) và tương quan (correlation).
Mục lục bài viết
Percentile – một khái niệm quan trọng trong thống kê cho khoa học dữ liệu
Percentile hay tiếng Việt gọi là bách phân vị (?!) là phần trăm số phần từ nhỏ hơn phần tử đã được chỉ định. Ở đây cần tránh nhầm lẫn với khái niệm phần trăm (percentage) nhé. Để dễ hiểu thì hãy cùng tìm hiểu ví dụ dưới đây.
Giả sử mình có một mẫu dữ liệu
X = {1, 3, 5, 7, 9, 11, 15, 16, 17, 19, 20} n = 11 phần tử.
Để tính được percentile của 1 phần tử ở vị trí thứ m nào đó, ta áp dụng công thức:
[math]P_m = \frac{m}{n+1}\times100[/math]
Vậy nếu tính percentile của phần tử có giá trị 16 ở vị trí thứ 8 sẽ là:
[math]P_8 = \frac{8}{11+1}\times100=66.67\%[/math]
Từ đó ta cũng sẽ có công thức suy ngược, ví dụ: phần tử nào có percentile là 25%? Phần tử đó sẽ ở vị trí thứ m, được tính là
[math]m = \frac{P_m}{100}*(n+1)=\frac{25}{100}\times(11+1) = 3[/math]
Vậy phần tử đó ở vị trí thứ 3, có giá trị là: 5
Từ đây chúng ta có thể thấy, giá trị có percentile 50% chính là trung vị của mẫu. Vậy những giá trị có percentile 25% và 75% thì như thế nào?
>>>> Xem thêm: Ánh sáng xanh không làm bạn mất ngủ như bạn thường nghĩ
Số phần tư và IQR
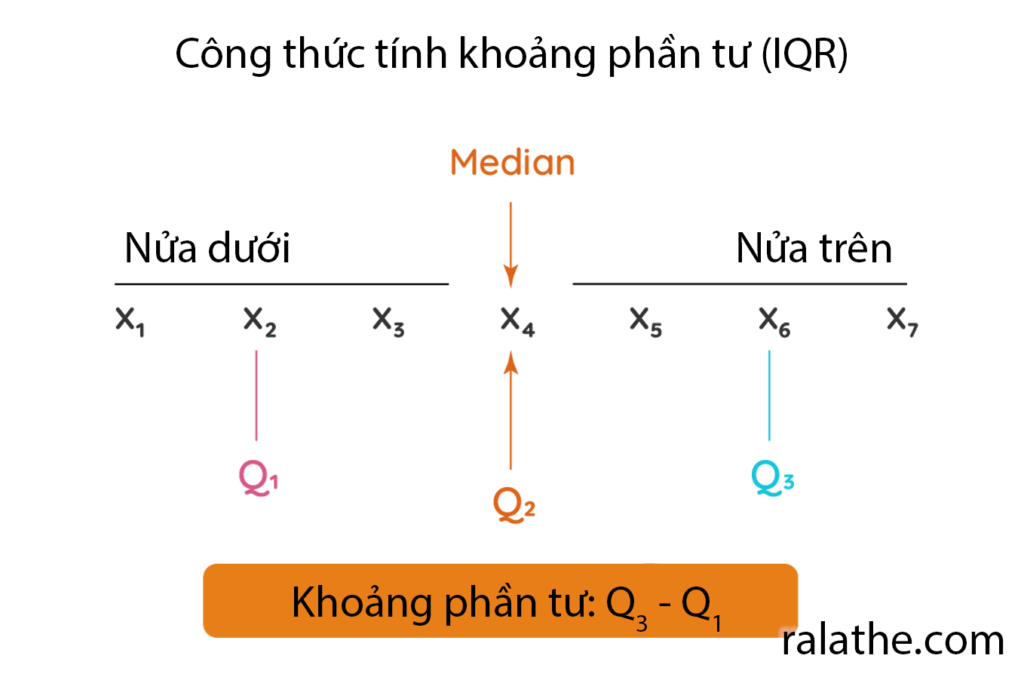
Trong thống kê cho khoa học dữ liệu hay data science, giá trị 25% và 75% percentile được gọi là số phần tư, vì nó chia mẫu dữ liệu của chúng ta ra thành 4 phần bằng nhau, mỗi phần 25%. Các phần này được ký hiệu là:
- 25% là Q1 (quatile 1 hay phần tư thứ nhất)
- 50% là Q2 (quatile 2 hay phần tư thứ hai)
- 75% là Q3 (quatile 3 hay phần tư thứ ba)
Và vì thế, các giá trị nằm trong khoảng từ Q1 đến Q3 được gọi là phạm vi phần tư hay interquatile range (IQR). Các giá trị nằm trong khoảng IQR sẽ không bị ảnh hưởng bởi các giá trị ngoại lệ, tất nhiên rồi!
Lower và upper fence trong thống kê cho khoa học dữ liệu
Làm thế nào để loại những kẻ ngoại đạo (outlier) này? Chúng ta sẽ dùng một kỹ thuật được gọi là “bao rào” (từ này do mình tự nghĩ ra).
Loại các outlier
Trong kỹ thuật bao rào này, chúng ta sẽ tính toán “rào dưới” (lower fence – LF) và “rào trên” (upper fence – UF). Giá trị này được tính như sau:
[math]LF = Q1 – 1.5 \times IQR[/math]
[math]UF = Q3 + 1.5 \times IQR[/math]
Những số nằm ngoài 2 rào này được gọi là các outlier (hay các số ngoại lệ nhưng mình gọi chúng là những kẻ ngoại đạo – mình thích từ này ghê).
Ví dụ: cho mẫu có các giá trị sau:
X = {29, 179, 180, 201, 300, 301, 304, 350, 399, 401, 455, 501, 503, 540, 543, 549, 560, 561, 562, 563, 569, 570, 599, 601, 603, 650, 701, 703, 704, 709, 713, 733, 745, 801, 900, 982, 983, 985, 999, 1001, 1002, 1003, 1009, 1100, 1101, 1102, 1103, 1109, 1201, 1301, 1399, 1400, 1501, 1599, 1699}, n = 55
Bạn tìm được đâu là outlier không?
Đầu tiên chúng ta sẽ sắp xếp lại dãy số này từ bé đến lớn (nếu chưa sắp xếp). Tiếp theo chúng ta sẽ tính Q1, Q2, Q3, IQR, LF, UF (các bạn tự tính nhé)
- Q1 = 540
- Q2 = 703 (median)
- Q3 = 1003
- IQR = 463
- LF = -154.5
- UF = 1697.5
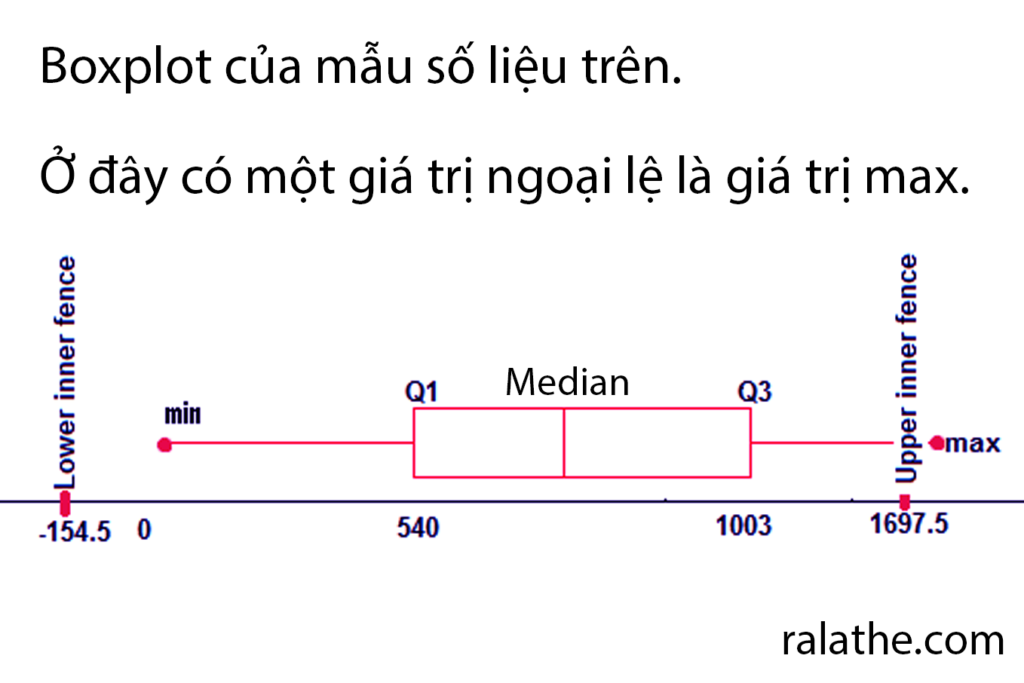
Những giá trị nằm ngoài khoảng LF tới UF được gọi là các outlier. Ở đây chúng ta có outlier là 1699. Quá dễ phải không!
Boxplot
Để biểu diễn sự phân bố của các giá trị, chúng ta có thể dùng biểu đồ dạng boxplot. Khi nhìn vào boxplot, ta sẽ thấy ngay được những giá trị quan trọng, bao gồm median, Q1, Q3, min, max của mẫu.
Chúng ta có thể vẽ boxplot với python như sau:
from scipy import stats
import matplotlib.pyplot as plt
## Dữ liệu mẫu
x = [29, 179, 180, 201, 300, 301, 304, 350, 399, 401, 455, 501, 503, 540, 543, 549, 560, 561, 562, 563, 569, 570, 599, 601, 603, 650, 701, 703, 704, 709, 713, 733, 745, 801, 900, 982, 983, 985, 999, 1001, 1002, 1003, 1009, 1100, 1101, 1102, 1103, 1109, 1201, 1301, 1399, 1400, 1501, 1599, 1699]
IQR = stats.iqr(x)
print(IQR)
## Chiều cao của boxplot là IQR
plt.boxplot(x)
plt.show()Nếu dùng R thì code sẽ là:
## Tạo mẫu số liệu
x = c(29, 179, 180, 201, 300, 301, 304, 350, 399, 401, 455, 501, 503, 540, 543, 549, 560, 561, 562, 563, 569, 570, 599, 601, 603, 650, 701, 703, 704, 709, 713, 733, 745, 801, 900, 982, 983, 985, 999, 1001, 1002, 1003, 1009, 1100, 1101, 1102, 1103, 1109, 1201, 1301, 1399, 1400, 1501, 1599, 1699)
## Vẽ boxplot
boxplot(x,data=x)Kết quả sẽ được như thế này:
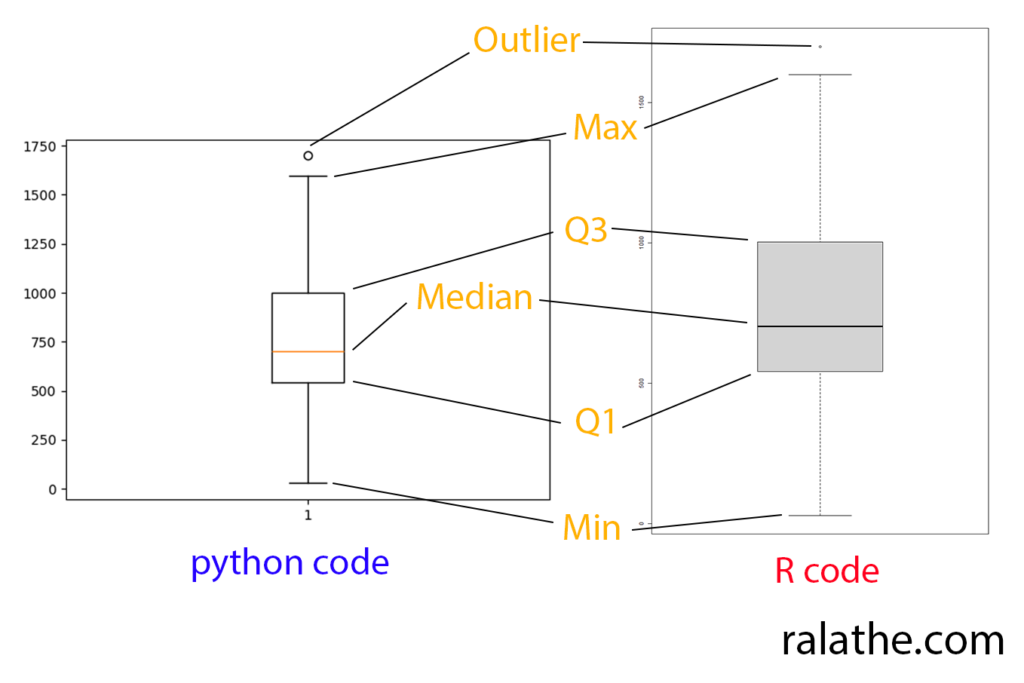
Đồng phương sai – covariance
Đồng phương sai (tiếng anh là covariance) là một khái niệm quan trọng trong thống kê cho khoa học dữ liệu. Đồng phương sai giúp ta nhận định về sự liên hệ giữa hai mẫu số liệu.
Ví dụ: ta có 2 mẫu số liệu như sau:
Độ tuổi của dân số: X = {18, 20, 25, 30, 33, 38, 40, 42, 45, 50, 53, 56} n = 12
Số tiền kiếm được (đơn vị triệu đồng): Y = {3, 5, 6, 8, 10, 12, 12, 15, 16, 18, 19, 22) n = 12
Bây giờ nếu ta muốn biết liệu có sự liên hệ nào giữa độ tuổi và sống tiền kiếm được hay không thì làm thế nào? Đồng phương sai chính là một cách xem xét.
Ta đã biết, phương sai của mẫu số liệu X có công thức như được đề cập ở bài 3.1 trong series này.
[math]s_x^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (x_i – \bar{x})^2[/math]
Công thức này có thể được viết lại là:
[math]s_x^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (x_i – \bar{x})(x_i – \bar{x})[/math]
Và phương sai của mẫu số liệu Y (số tiền kiếm được) sẽ là:
[math]s_y^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (y_i – \bar{y})^2[/math]
Do đó, khi tính đồng phương sai, kí hiệu là cov(x,y), ta sẽ thay một vế [math](x_i – \bar{x})[/math] thành [math](y_i – \bar{y})[/math] thể hiện cho sự tương quan của 2 biến. Và ta có công thức đồng phương sai như bên dưới:
[math]cov(x,y) = \frac{1}{n-1}\sum\limits_{i=1}^n (x_i – \bar{x})(y_i – \bar{y})[/math]
Tuy nhiên, cov(x,y) là một số không có giới hạn, do đó người ta thường cố gắng chuẩn hóa nó lại và đưa nó về khoảng (-1,1). Cách làm như thế gọi là tương quan và hệ số cov(x,y) lúc này được gọi là hệ số tương quan.
Trong thống kê cho khoa học dữ liệu, có rất nhiều hệ số tương quan. Trong bài này chúng ta sẽ tìm hiểu về tương quan Pearson, một tương quan rất hay được sử dụng trong thống kê.
Tương quan Pearson
Hệ số tương quan pearson (pearson correlation coefficient) dùng để mô tả sự tương quan tuyến tính của 2 tập dữ liệu. Hệ số này sẽ được tính theo công thức:
[math]\rho=\frac{cov(x,y)}{\sigma_x\sigma_y}[/math]
Trong đó thì [math]\rho[/math] (đọc là rô) là hệ số tương quan Pearson. [math]\sigma_x[/math] và [math]\sigma_y[/math] là độ phân tán của mẫu số liệu X và Y.
Nhìn vào công thức này ta có thể thấy ngay được:
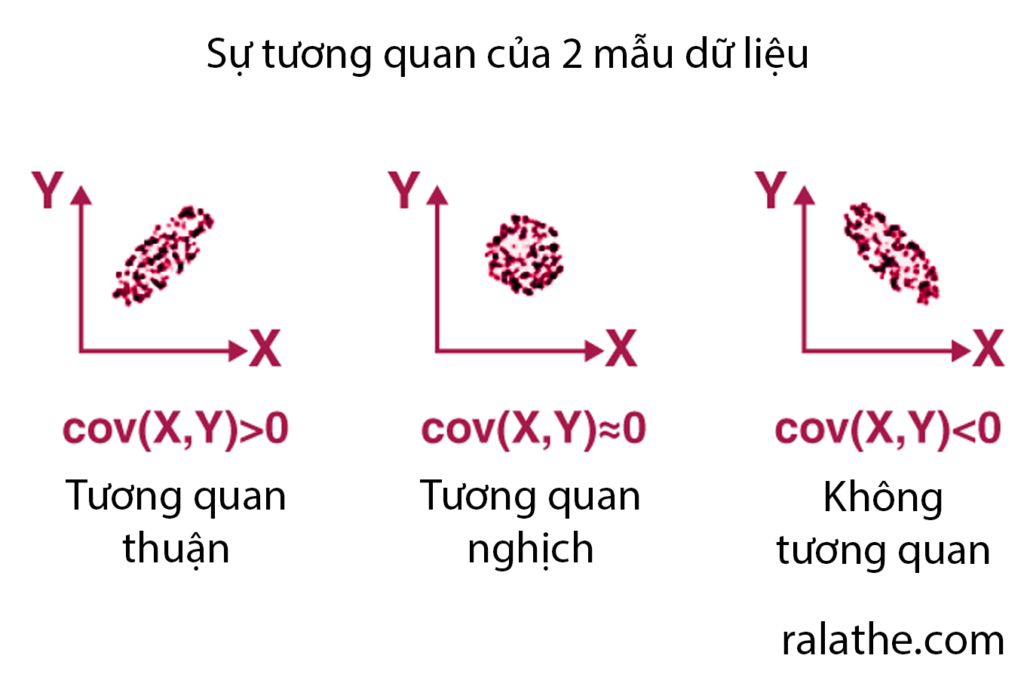
- Nếu là tương quan nghịch (X tăng, Y giảm và ngược lại) thì [math]\rho < 0[/math]
- Nếu là tương quan thuận (X tăng, Y tăng và ngược lại) thì [math]\rho > 0[/math]
- Nếu không có sự tương quan (phân bố ngẫu nhiên) thì [math]\rho = 0[/math]
Vậy nếu [math]\rho[/math] càng tiến dần về 2 đầu mút (-1 và 1) thì sự tương quan càng chặc chẽ.
Ta có thể tính hệ số Pearson trong python bằng code:
## load thư viện pandas
import pandas as pd
## Tạo mẫu dữ liệu
x = [18, 20, 25, 30, 33, 38, 40, 42, 45, 50, 53, 56]
y = [3, 5, 6, 8, 10, 12, 12, 15, 16, 18, 19, 22]
## Tạo data frame
df = pd.DataFrame({'x':x, 'y':y})
## Tính correlation
df.corr()
## ---- Kết quả ---- ##
x y
x 1.000000 0.992803
y 0.992803 1.000000Ở đây ta được ma trận tương quan giữa X và Y, bạn chỉ cần liên quan đến đường chéo phụ là đủ (nó tự tương quan với nó nên đường chéo chính luôn là 1)
Hoặc bằng R:
## Tạo mẫu số liệu
x = c(18, 20, 25, 30, 33, 38, 40, 42, 45, 50, 53, 56)
y = c(3, 5, 6, 8, 10, 12, 12, 15, 16, 18, 19, 22)
## Pearson correlation
cor(x,y, method = "pearson")
## ---- Kết quả ------ ##
[1] 0.992803Tuy nhiên, trong một vài trường hợp thì hệ số Pearson không thể hiện đúng tính chất của sự tương quan (vì là tuyến tính), ví dụ như trường hợp dưới đây:
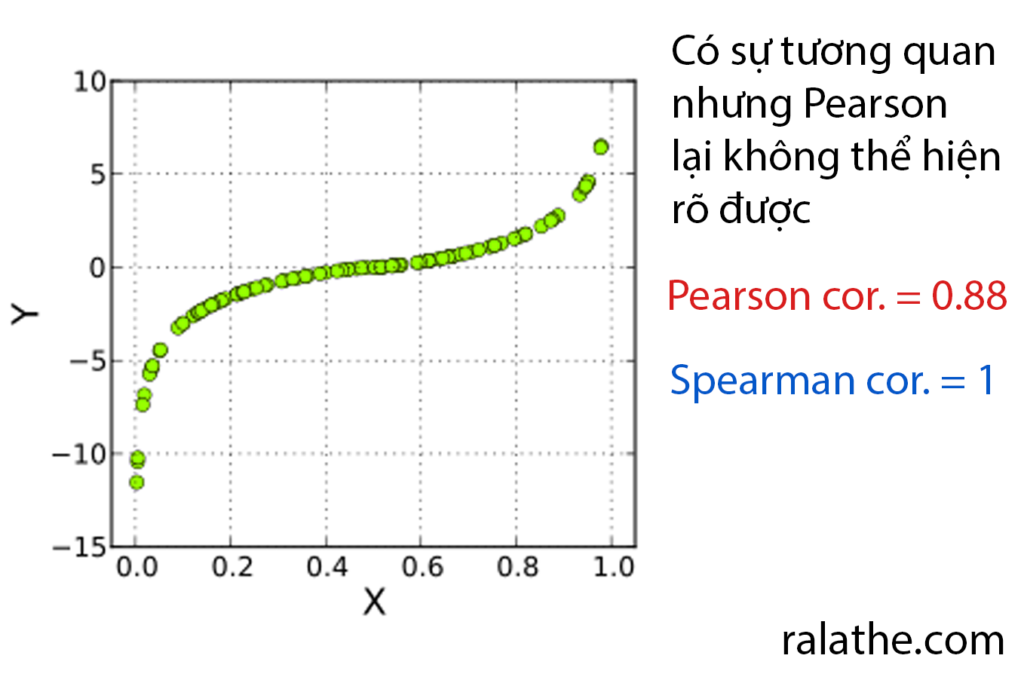
Lúc này ta sẽ dùng một hệ số tương quan khác. Nhưng nó sẽ là trong bài sau nhé!
