Trong bài 3.1, chúng ta đã tìm hiểu về hai giá trị đại diện khác của mẫu số liệu thường thấy trong thống kê cho khoa học dữ liệu, đó là trung vị và mode. Trong phần 2 của bài 3 này, chúng ta sẽ cùng tìm hiểu một khái niệm cực kỳ quan trọng trong thống kê, đó là phân bố chuẩn (normal distribution).
Hãy cùng bắt đầu nhé!
Mục lục bài viết
Phân bố chuẩn trong thống kê cho khoa học dữ liệu
Khi nhắc đến mode, chúng ta sẽ nghĩ ngay đến tần suất xuất hiện của một giá trị trong mẫu. Hãy cùng xét bảng sau:
| Giá trị | Tần suất |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 4 |
| 7 | 3 |
| 8 | 2 |
| 9 | 1 |
Cho những ai chưa biết thì bảng này có thể được biểu diễn dưới dạng tập hợp các giá trị của mẫu X như sau:
X = [1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,7,7,7,8,8,9]
Histogram
Bây giờ, chúng ta sẽ vẽ biểu đồ phân phối của những giá trị xem nó sẽ như thế nào nhé! Ở đây mình sử dụng code python cho biểu đồ này:
import matplotlib.pyplot as plt
# dữ liệu đầu vào (mẫu X)
X = [1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,7,7,7,8,8,9]
# Tạo graph histogram
plt.hist(X, bins=9, color='skyblue', edgecolor='black')
# Thêm nhãn và tiêu đề
plt.xlabel('Giá trị')
plt.ylabel('Tần suất')
plt.title('Biểu đồ histogram của mẫu X')
# Hiện biểu đồ
plt.show()Ta sẽ được một biểu đồ như thế này:
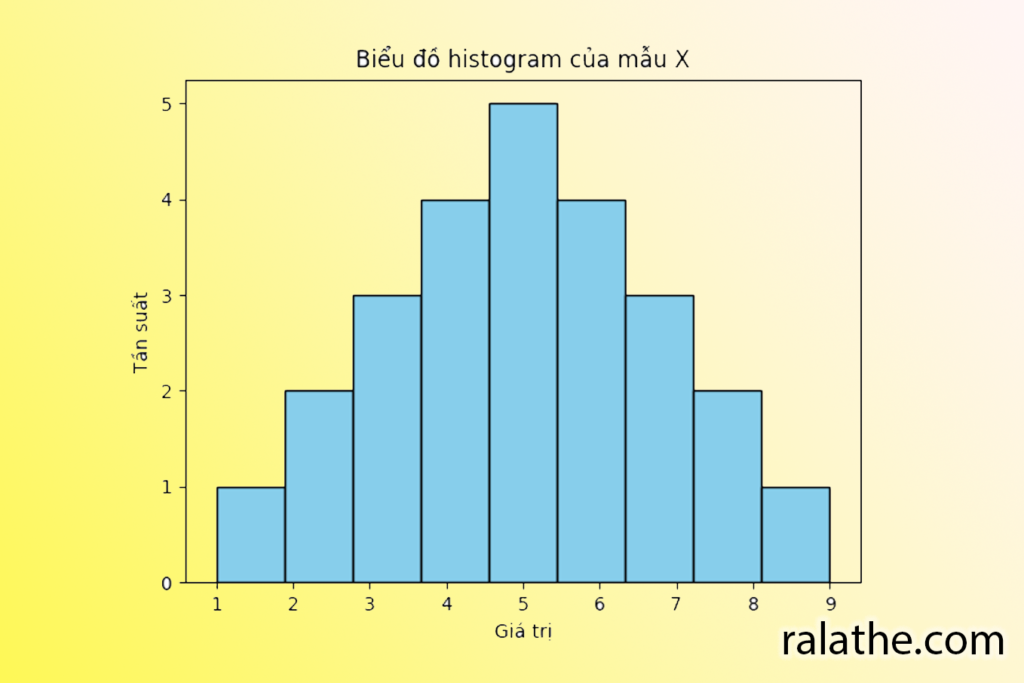
Trong data science, Biểu đồ này được gọi là histogram hay biểu đồ tần suất. Đây cơ bản là một cách trực quan để thể hiện sự phân bố của tần suất của các giá trị trong mẫu số liệu.
Bây giờ, nếu ta tăng số lượng giá trị của mẫu lên, ví dụ 1000. Chúng ta sẽ dùng numpy để tạo ra những số ngẫu nhiên và vẽ histogram của nó xem như thế nào nhé.
import matplotlib.pyplot as plt
import numpy as np
# Tạo ra những giá trị ngẫu nhiên cho mẫu làm dữ liệu đầu vào
data = np.random.randn(1000) # tạo ra những số ngẫu nhiên theo phân phối chuẩn
# Tạo histogram
plt.hist(data, bins=30, color='greenyellow', edgecolor='black')
# Thêm nhãn và tiêu đề
plt.xlabel('Giá trị')
plt.ylabel('Tần suất')
plt.title('Biểu đồ histogram của mẫu data')
# Hiện biểu đồ
plt.show()Chúng ta sẽ có được biểu đồ như hình bên dưới:
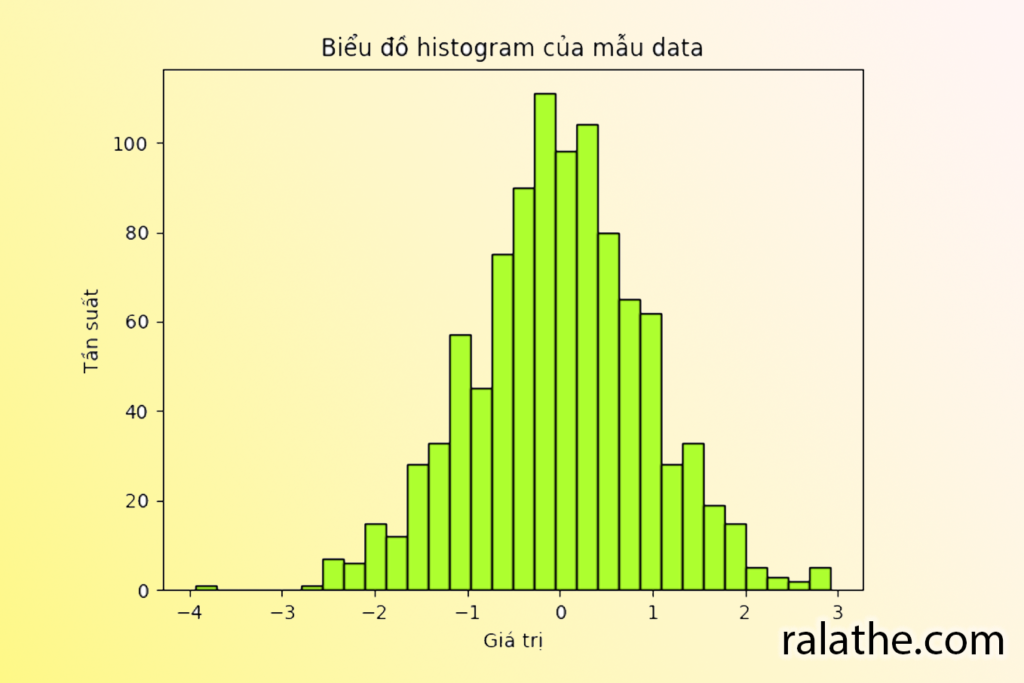
>>>> Xem thêm: Sửa lỗi cơ bản trong R cho các bạn lần đầu sử dụng
Phân bố Gaussian – một phân bố quan trọng trong thống kê cho khoa học dữ liệu
Bây giờ chúng ta sẽ sửa lại code một chút, và thêm vào đó đường biểu diễn mật độ (density plot) của histogram vừa rồi:
import matplotlib.pyplot as plt
import seaborn as sns # Thêm vào thư viện seaborn vào
import numpy as np
# Tạo ra những giá trị ngẫu nhiên cho mẫu làm dữ liệu đầu vào
data = np.random.randn(1000)
# Thêm đường mật độ (density plot) cho histogram này
sns.histplot(data, bins=30, kde=True, color='red', edgecolor='black')
# Thêm nhãn và tiêu đề
plt.xlabel('Giá trị')
plt.ylabel('Tần suất')
plt.title('Biểu đồ histogram của mẫu data + density plot')
# Hiện biểu đồ
plt.show()Chúng ta sẽ được biểu đồ như thế này:
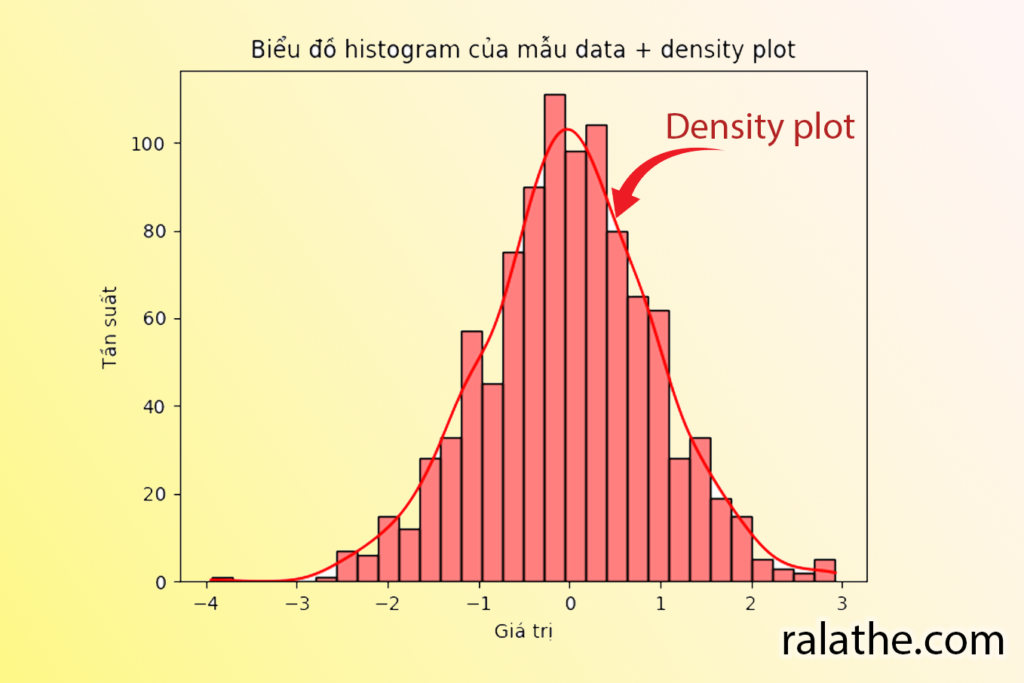
Các bạn có nhận thấy rằng đường màu đỏ (density plot) có dạng giống như một cái chuông không? Chính vì thế mà nó được gọi là biểu đồ chuông (bell curve) hay là biểu đồ phân bố chuẩn (normal distribution) hay còn gọi là Gaussian distribution.
Vậy phân phối chuẩn là gì? nó chính là phân bố xác suất xuất hiện của các giá trị trong quần thể (population). Các giá trị này có đặc điểm:
- Đối xứng qua mean
- Những dữ liệu ở càng gần mean thì có tần suất xuất hiện càng cao.
Đặc điểm của phân phối chuẩn
Phân phối chuẩn (thường được ký hiệu là N) được thể hiện qua 2 giá trị là mean và [math]\sigma[/math] (độ lệch chuẩn – SD). Phân phối chuẩn rất quan trọng trong lý thuyết trung tâm (central limit theorem – CLT).
>>>> Có thể bạn thích: nhìn chó giống chủ là chuyện đương nhiên
CLT – lý thuyết quan trọng trong thống kê cho khoa học dữ liệu
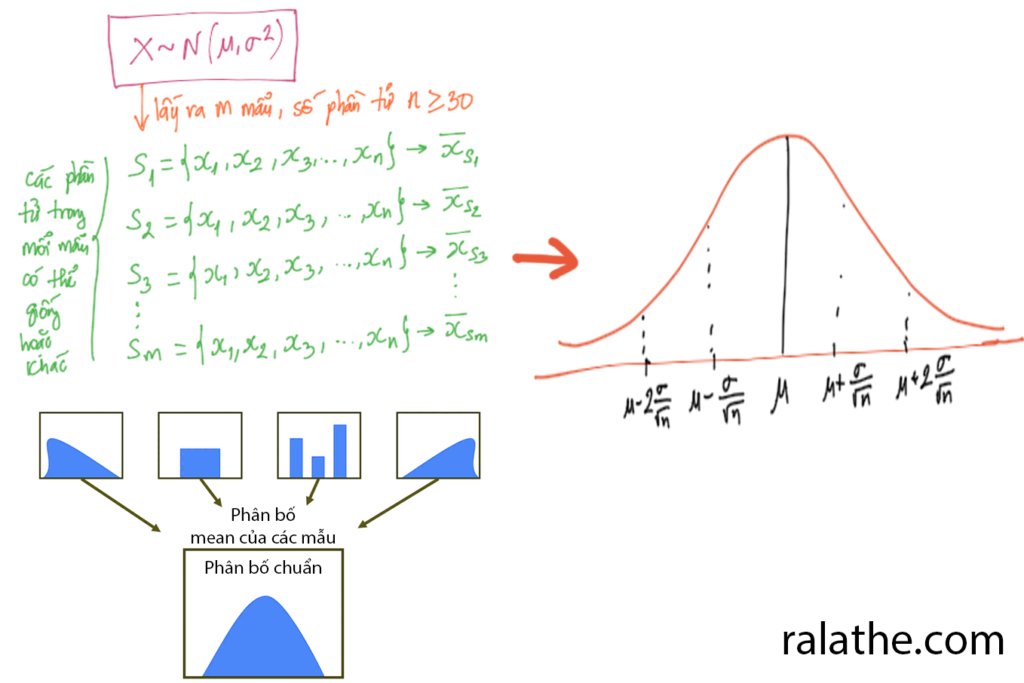
Giả sử mình có một quần thể X tuân theo phân phối chuẩn. Ký hiệu là: [math]X \sim \mathcal{N}(\mu,\,\sigma^{2})[/math]. Khi đó, nếu ta lấy ngẫu nhiên ra m mẫu (mỗi mẫu có số lượng phần từ [math]n \geq 30[/math]. Khi đó, Nếu ta lấy giá trị trung bình của tất cả m mẫu trên
[math]{\bar{x_1}, \bar{x_2}, \bar{x_3}, …, \bar{x_m}}[/math]
và đem vẽ ra thành đồ thị, thì nó sẽ tạo ra một đồ thị chuẩn (hình chuông). Đồ thị này có giá trị trung bình bằng [math]\mu[/math] (trung bình của cả quần thể) và phương sai là [math]\frac{\sigma^2}{n}[/math]. Có thể ký hiệu là [math](\mu,\frac{\sigma^2}{n})[/math].
>>>> Bạn có biết: Thực ra ánh sáng xanh không làm bạn mất ngủ
Tính chất của phân phối chuẩn
Phân phối chuẩn có một số tính chất thú vị sau:
- Trong phân phối chuẩn thì mean = median = mode
- Phân phối đối xứng nhau và có trục là đường thẳng đi qua mean.
- Độ rộng của nó được định nghĩa bằng [math]\sigma[/math]
- Chính vì thế mà mọi phân phối chuẩn đều có thể được định nghĩa bằng mean và SD.
Luật phân bố xác suất
Trong phân bố chuẩn có luật phân bố quan trọng như sau:
- Có 68.2% giá trị quan sát được xuất hiện trong khoảng [math]\mu \pm \sigma[/math].
- Có 95.4% giá trị quan sát được xuất hiện trong khoảng [math]\mu \pm 2\sigma[/math].
- Có 99.8% giá trị quan sát được xuất hiện trong khoảng [math]\mu \pm 3\sigma[/math].
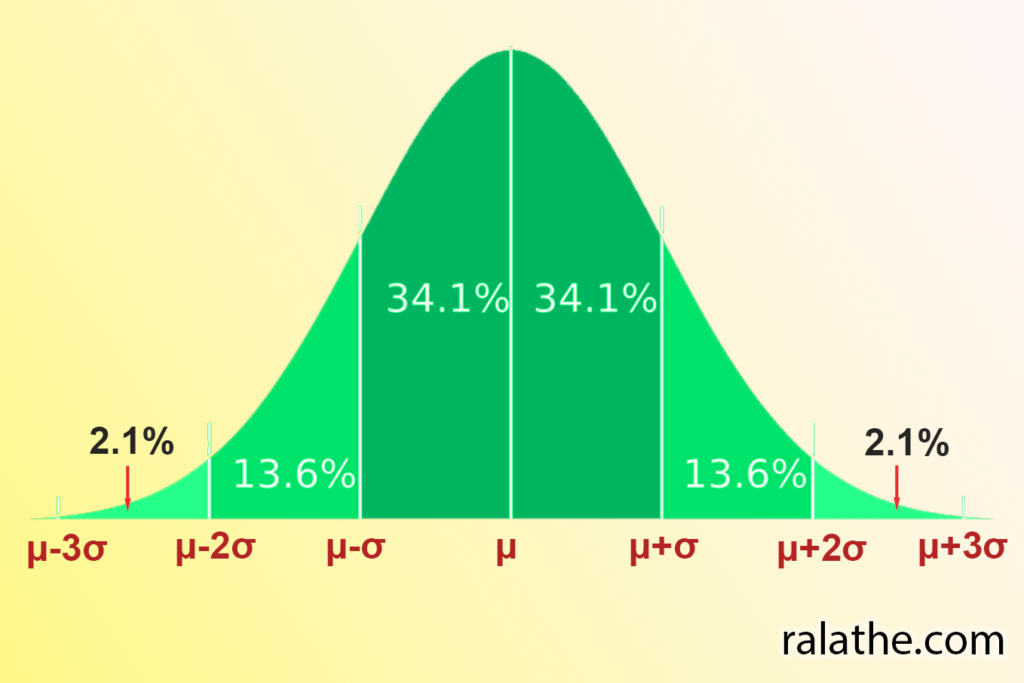
Đây là luật phân bố xác suất quan trọng mà chúng ta cần nhớ để có thể áp dụng trong các trường hợp thống kê cho khoa học dữ liệu sau này được nhuần nhuyễn hơn.
>>>> Bạn có quan tâm: ứng dụng và cách làm vaseline thiên nhiên
Độ lệch (skewness)
Độ lệch biểu mức độ bất đối xứng của phân phối chuẩn. Phân phối chuẩn có độ lệch bằng 0 (2 đuôi của phân phối như nhau).
Tuy nhiên, nếu phần đuôi bên trái dài hơn bên phải (chuông nghiêng về bên phải) thì ta nói phân phối có độ lệch âm hay lệch trái. Ngược lại, nếu đuôi bên phải dài hơn bên trái (chuông nghiêng về bên trái) thì ta nói phân phối có độ lệch dương hay lệch phải.
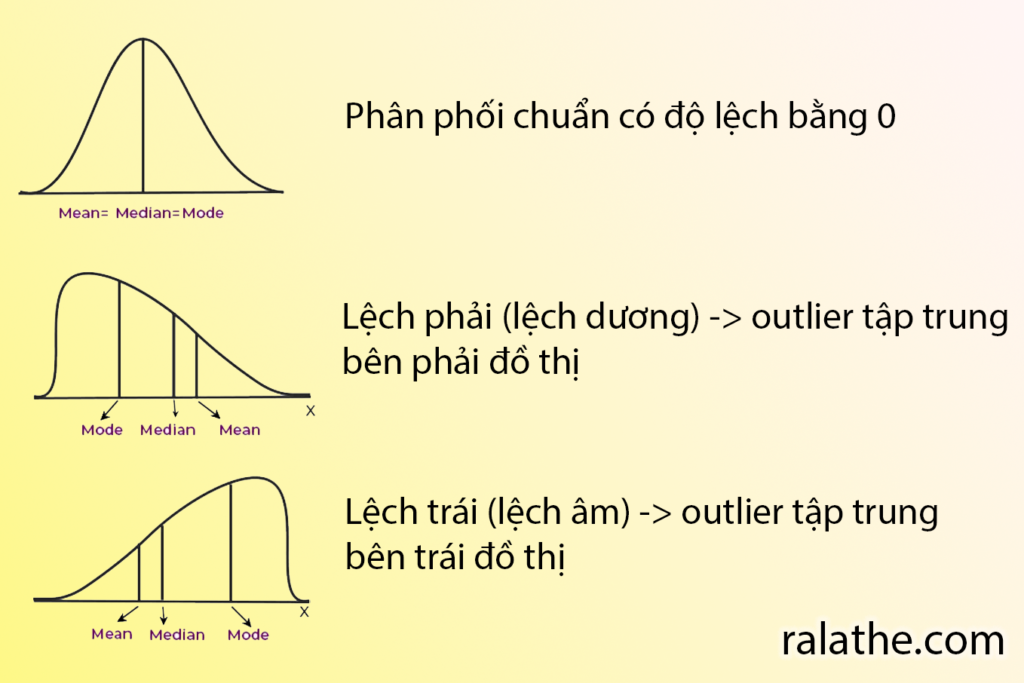
Độ lệch dùng để làm gì? Nó cho phép chúng ta đánh giá các kẻ ngoại đạo (outlier) nằm về phía bên nào của phân phối. Nếu là lệch phải, nghĩa là các outlier sẽ tập trung nhiều về phía phải của đồ thị phân phối chuẩn và ngược lại.
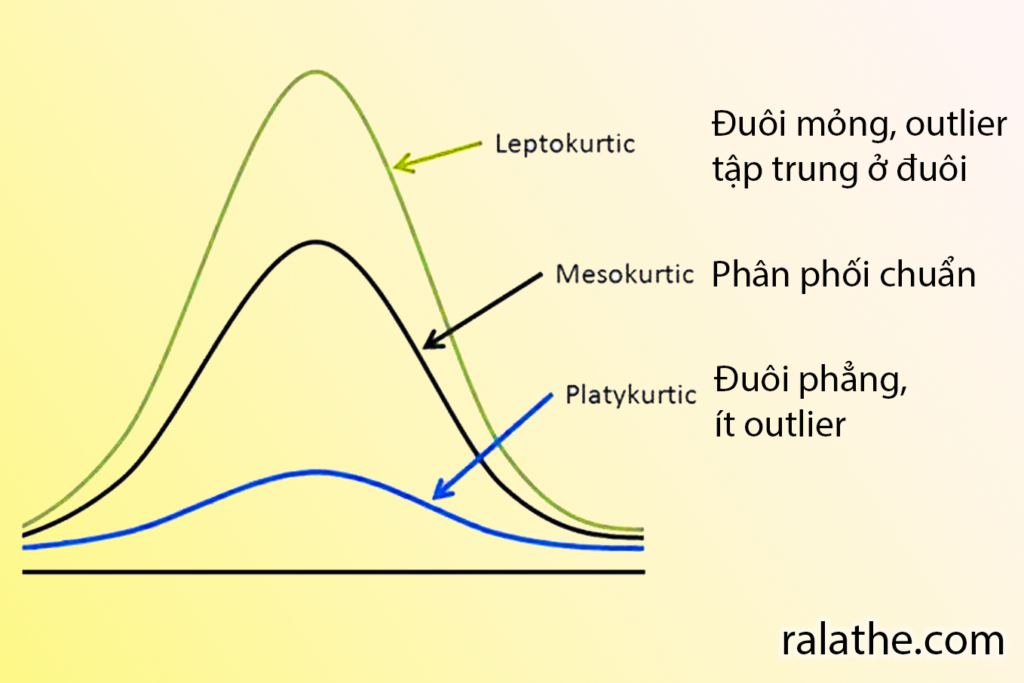
Độ nhọn (kurtosis)
Độ nhọn cho biết độ dày của phần đuôi trong phân phối. Phân phối chuẩn có độ nhọn là 3 (mesokurtic). Nếu phân phối có độ nhọn >3 thì phân phối đó có nhiều outlier tập trung ở đuôi của đồ thị hay gọi là leptokurtic. Nếu độ nhọn < 3 thì phân phối có đuôi phẳng (flat tail – ít outlier), còn được gọi là platykurtic.
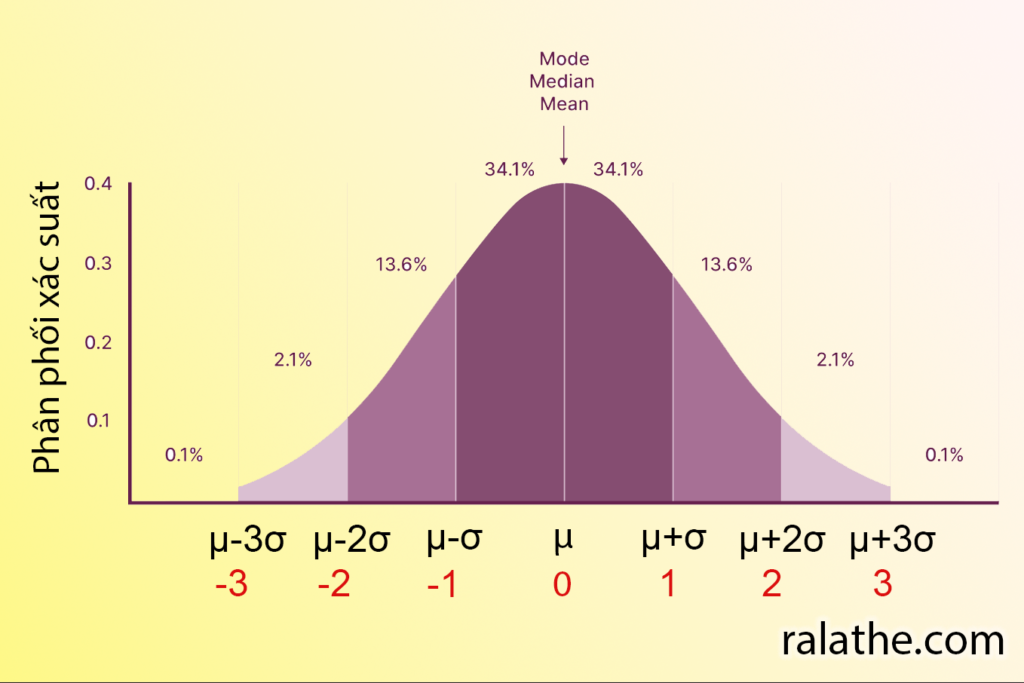
Điểm Z (Z-score)
Điểm Z cho chúng ta biết chính xác khoảng cách từ một điểm giá trị đến mean là bao nhiêu. Từ biểu đồ phân phối chuẩn ở trên, nếu chúng ta đưa [math]\mu[/math] về 0 và [math]\sigma[/math] về 1 thì ta sẽ có được biểu đồ với các giá trị như hình bên dưới. Biểu đồ này được gọi là biểu đồ chuẩn của phân phối chuẩn (standard normal distribution – SND).
Cách tính điểm Z
Điểm Z của một giá trị [math]x[/math] nào đó sẽ được tính theo công thức sau:
[math]z = \frac{x – \mu}{\sigma}[/math]
Tính chất quan trọng của điểm Z
Từ công thức trên chúng ta sẽ thấy điểm Z có một số tính chất sau:
- Điểm Z của mean bằng 0 (chắc chắn rồi)
- Nếu Z < 0 thì giá trị của chúng ta ở dưới mean
- Nếu Z > 0 thì giá trị ở trên mean
- Một giá trị được cho là bất thường nếu Z < -3 hoặc Z > 3 (chắc không?)
>>>> Xem lại: thống kê cho khoa học dữ liệu, bài 1: khía niêm cơ bản
Tại sao lại tính điểm Z – ứng dụng của điểm Z
Tính điểm Z có hai ứng dụng:
- Chuẩn hóa số liệu (standardization)
- So sánh các số liệu có phân phối chuẩn nhưng khác nhau về mean và SD
Ví dụ về trường hợp so sánh giữa các mean: Chẳng hạn, bạn đi thi được một số điểm như sau:
| Môn học | Điểm bạn đạt được | Trung bình của toàn khối | Độ lệch chuẩn của khối |
| Toán | 8 | 7 | 1 |
| Lý | 7 | 5 | 2 |
| Tiếng Anh | 9 | 8 | 3 |
Làm thế nào bạn biết được mình học môn nào khá hơn? Lúc này điểm Z sẽ giúp bạn.
Điểm Z của toán là: [math]Z_T = \frac{8 – 7}{1} = 1[/math]
Điểm Z của lý là: [math]Z_L = \frac{7 – 5}{2} = 1[/math]
Điểm Z của tiếng anh là: [math]Z_{TA} = \frac{9 – 8}{3} = \frac{1}{3}[/math]
Từ đây bạn thấy [math]Z_T = Z_L > Z_{TA}[/math] nên bạn có thể nói là mình học toán với lý như nhau và khá hơn học tiếng anh. Bạn thấy đấy, đôi khi điểm cao hơn chưa chắc mình đã học khá hơn.
Video bài giảng thống kê cho khoa học dữ liệu | bài 3
Bài 3.2 này bắt đầu từ phút 13:46 của video bài giảng nhé!
PS. Bài 3 này dài quá, dự định ban đầu là làm những bài tham khảo ngắn thôi, cho dễ đọc, dễ nhớ mà sao càng viết lại càng thấy thiếu thiếu sao đó. Hi vọng những bài sau có thể viết ngắn hơn.
