Ở bài 2 của series thống kê cho khoa học dữ liệu (data science) chúng ta đã tìm hiểu về giá trị trung bình của xu hướng trung tâm. Trong bài này, chúng ta tiếp tục tìm hiểu thêm 2 giá trị có thể làm giá trị đại diện cho mẫu thống kê của mình. Đó là trung vị (median) và mode. Tiếp đó chúng ta sẽ cùng nhau tìm hiểu về độ phân tán của dữ liệu để từ đó có thể xây dựng được phân bố của dữ liệu.
Hãy cùng bắt đầu chuỗi series bài học cơ bản này nhé!
Mục lục bài viết
Giá trị đại diện khác trong thống kê cho khoa học dữ liệu
Ở bài trước, chúng ta đã tìm hiểu một giá trị đại diện quan trong thống kê, đó là mean và các công thức tính mean khác nhau trong từng trường hợp cụ thể.
Lý do cần có những giá trị đại diện khác ngoài mean
Tuy nhiên, việc sử dụng giá trị mean để làm đại diện sẽ gặp phải một bất lợi, đó là nếu trong mẫu có các phần tử bất thường, lớn bất thường hoặc nhỏ bất thường, tiếng anh gọi là giá trị outlier (những kẻ ngoại đạo 🤣).
Ví dụ: xét một mẫu có các giá trị như sau: X = {9, 5, 2, 1, 3, 8, 6, 4, 7, 100} n = 10.
Nếu tính trung bình cộng thì: mean = 14.5. Chúng ta nhận ra điều gì? Giá trị mean lớn hơn 9 giá trị trong toàn bộ mẫu. Như vậy thì có hợp lý không chị chọn mean làm giá trị đại diện cho toàn bộ giá trị trong mẫu này?
Hoàn toàn không hợp lý chút nào, đúng không?
Do đó, để đại diện cho mẫu này, chúng ta không thể sử dụng mean được mà cần phải dùng một đại lượng khác.
Và giá trị làm cho mean mất đị vị trí giá trị đại diện của mình chính là outlier, ở ví dụ này là phần tử [math]x_{10} = 100[/math].
Median (trung vị)
Trong thống kê cho khoa học dữ liệu, ngoài mean ra, thì median (Med) hay trung vị còn thường xuyên được dùng làm giá trị đại diện vì median khắc phục được hạn chế của mean. Đó chính là không bị ảnh hưởng bởi những kẻ ngoại đạo (outlier) kia.
Median chính là số ở giữa, nghĩa là giá trị có vị trí nằm ở trung tâm của mẫu. Cách tính median như thế nào?
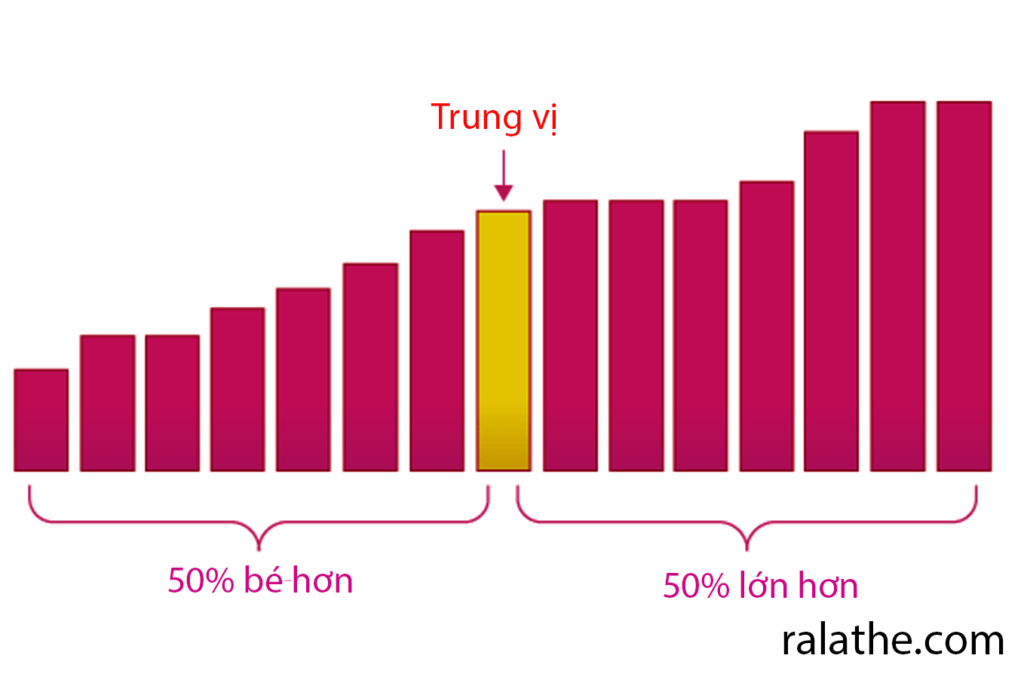
Cách tính trung vị trong thống kê cho khoa học dữ liệu
Xét lại ví dụ tập số lúc nãy: X = {9, 5, 2, 1, 3, 8, 6, 4, 7, 100} n = 10.
Để tìm được median, đầu tiên, chúng ta sắp xếp lại tập giá trị này theo thứ tự từ thấp đến cao (hoặc từ cao đến thấp tùy bạn, dù sao thì nó cũng là số nằm ở giữa của dãy số mà).
>> X = (1, 2, 3, 4, 5, 6, 7, 8, 9, 100} n = 10. (Việc xáo trộn các số trong mẫu này lúc đầu là có chủ ý đấy 😆)
Tiếp theo chúng ta tìm median theo công thức này nhé!
1. Trường hợp 1: Nếu n lẻ
Trung vị là số ở vị trí thứ [math]\frac{n+1}{2}[/math]
ví dụ: X = (1, 3, 5, 7, 8, 9, 10, 11, 12, 99,100} n = 11 -> vị trí thứ [math]\frac{n+1}{2} = \frac{11+1}{2}=6[/math]
Trung vị là: Med = 9.
2. Trường hợp 2: Nếu n chẵn
Trung vị là số ở vị trí thứ [math]\frac{\frac{n}{2}+(\frac{n}{2}+1)}{2}[/math]
Vì n chẵn nên có tới 2 số ở giữa ở vị trí n/2 và (n+1)/2 nên ta lấy trung bình của 2 số này, sẽ được trung vị.
Ví dụ: cho tập X = (1, 3, 5, 7, 8, 9, 10, 11, 12,100} n = 10 -> Vị trí thứ [math]\frac{\frac{n}{2}+(\frac{n}{2}+1)}{2}[/math] = [math]\frac{\frac{10}{2}+(\frac{10}{2}+1)}{2} = \frac{5+6}{2} = 5.5[/math] (lưu ý, đây là vị trí của số hạn, không phải là giá trị)
Trung vị là Med = [math]\frac{8+9}{2}=8.5[/math]
Quay lại ví dụ ở trên X = (1, 2, 3, 4, 5, 6, 7, 8, 9, 100} n = 10. Do n chẵn nên trung vị của nó sẽ là: Med = (5+6)/2 = 5.5
Các bạn có thể dùng python để tính trung vị như sau:
import numpy as np
sample = [1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2]
trungVi = np.median(sample)
print(trungVi)
###(kết quả trả về)###
4.0Hoặc tính trong R sẽ là:
sample = c(1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2)
median(sample)
###(kết quả trả về)###
[1] 4Tính chất của trung vị
Như đã nói ở trên, do trung vị chỉ lấy giá trị ở vị trí chính giữa của mẫu, nên không bị ảnh hưởng bởi outlier, dù cho chúng có là bao nhiêu đi nữa thì cũng không ảnh hưởng đến giá trị của trung vị.
Chẳng hạn như trong ví dụ lúc đầu: X = (1, 2, 3, 4, 5, 6, 7, 8, 9, 100} n = 10. Ta thấy mean = 14.5 và med = 5.5. Rõ ràng, trong trường hợp này thì sử dụng med làm giá trị đại diện sẽ tốt hơn mean, phải không?
Mode (yếu vị)
Mode là giá trị có nhiều lần xuất hiện nhất trong mẫu số liệu của chúng ta, hay nói cách khác nghe có vẻ khoa học hơn là mode chính là giá trị có tần suất xuất hiện cao nhất (mật độ nhiều nhất) trong mẫu số liệu.
Ví dụ: cho mẫu số liệu X = {1, 1, 2, 5, 5, 3, 5, 1, 4, 5, 7} n = 11. Ta có thể thấy:
- Giá trị 1 xuất hiện 3 lần
- Giá trị 2, 3, 4, 7 mỗi giá trị xuất hiện 1 lần
- Giá trị 5 xuất hiện 4 lần
Giá trị 5 xuất hiện nhiều nhất, nên 5 chính là mode của tập giá trị này.
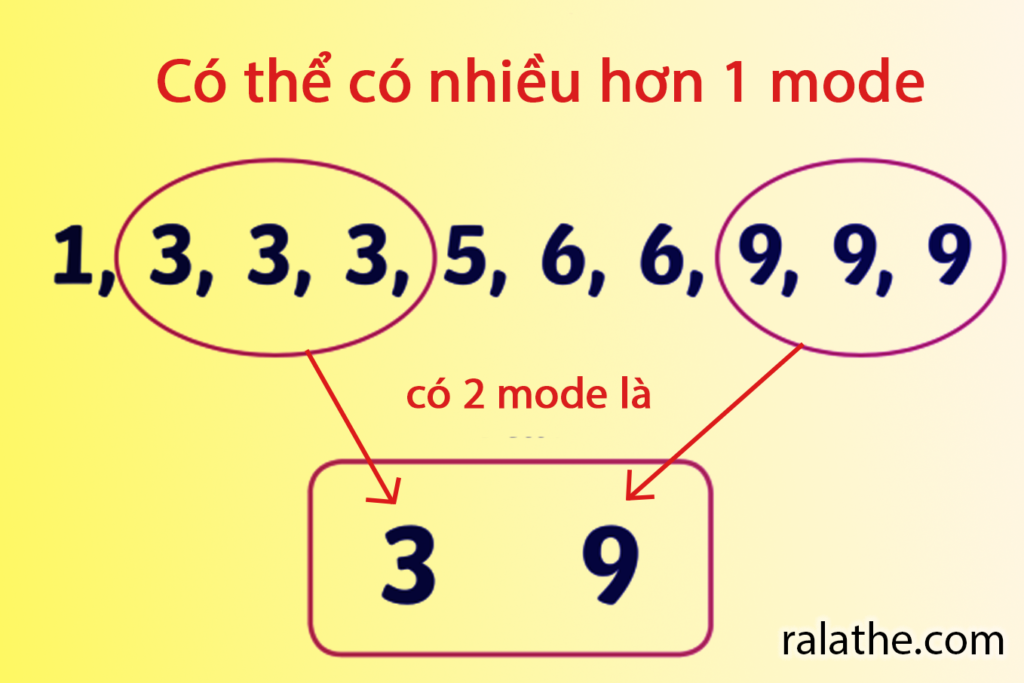
Để tính mode trong python, ta có thể dùng code sau:
from scipy import stats
sample = [1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2]
mode = stats.mode(sample)
print(mode)
###(kết quả trả về)###
ModeResult(mode=2, count=3)Ở đây, kết quả trả về 2 giá trị là mode và tần suất của nó. Nếu tìm thấy 2 mode, kết quả sẽ trả về mode có giá trị nhỏ hơn
Còn trong R, do R không có sẵn hàm tính mode, nên chúng ta có thể xây dựng hàm để tính như sau:
# Tạo hàm tính mode có tên là GetMode
GetMode = function(v) {
uniqv = unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Mẫu cần tính mode
sample = c(1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2)
# Tính toán và đưa ra giá trị mode.
result = GetMode(sample)
print(result)
###(kết quả trả về)###
[1] 2Cần lưu ý là ở đây chúng ta có 2 mode là 2 và 3. Tuy nhiên, do 2 xuất hiện trước nên nó sẽ trả về kết quả là 2.
Độ phân tán của dữ liệu
Độ lệch của dữ liệu chính là giá trị thể hiện cho khoảng cách của mỗi giá trị đến giá trị trung bình. Tuy nhiên, như đã đề cập đến ở bài trước, khi tính tổng khoảng cách từ các giá trị đến giá trị trung bình thì tổng độ lệch đó sẽ là 0. Do đó, nếu tính như vậy thì chẳng có ý nghĩa gì cả.
>>>> Có thể bạn thích: cách cài đặt Node JS để chạy website cá nhân
Độ lệch trung bình
Vậy nếu ta lấy giá trị tuyệt đối của tất cả các độ lệch (để loại giá trị âm) thì sao? Lúc này ta sẽ có được giá trị tổng các khoảng cách (chính là tổng độ lệch của tất cả giá trị đến trung bình). Nếu lấy tổng này chia cho tổng số phần tử thì ta sẽ được giá trị gọi là độ lệch trung bình (mean deviation – MD) hay độ lệch trung bình tuyệt đối (mean absolute deviation) do giá trị này được tính từ giá trị tuyệt đối. Công thức tính của MD như sau:
[math]MD = \frac{1}{n}(|x_1 – \bar{x}| + |x_2 – \bar{x}| + |x_3 – \bar{x}| + … + |x_n – \bar{x}|) = \frac{1}{n}\sum\limits_{i=1}^n |x_i – \bar{x}|[/math]
Từ đó ta có thể thấy, nếu dữ liệu phân tán cao (các giá trị rải rác) thì MD sẽ lớn và ngược lại. Tuy nhiên, có một vấn đề với MD, đó chính là dấu trị tuyệt đối. Để loại dấu trị tuyệt đối này, người ta sẽ bình phương nó lên. Và khi làm như vậy thì ta sẽ có được phân tán hay phương sai (variance). Công thức lúc này sẽ là:
[math]Variance = \frac{1}{n}((x_1 – \bar{x})^2 + (x_2 – \bar{x})^2 + (x_3 – \bar{x})^2 + … + (x_n – \bar{x})^2) =\frac{1}{n}\sum\limits_{i=1}^n (x_i – \bar{x})^2[/math]
Và khi lấy căn bậc hai của phương sai, ta sẽ được độ lệch chuẩn (standard deviation – SD). SD thường được viết là s nếu tính cho mẫu dữ liệu, và [math]\sigma[/math] nếu dùng cho cả quần thể (population)
[math]s =\sqrt{\frac{1}{n}\sum\limits_{i=1}^n (x_i – \bar{x})^2}[/math]
Phân tán bất thiên
Bất thiên (unbiased) nghĩa là không có thiên lệch, hay lệch lạc. Khi bạn chiết suất dữ liệu từ quần thể (population) ra những mẫu dữ liệu nhỏ hơn (samples) thì những mẫu dữ liệu này chính là một phần của quần thể đó. Do đó, dễ dàng thấy được là không có bất kỳ dữ liệu nào từ mẫu dữ liệu ta lấy ra nằm ngoài phạm vị của quần thể cả.
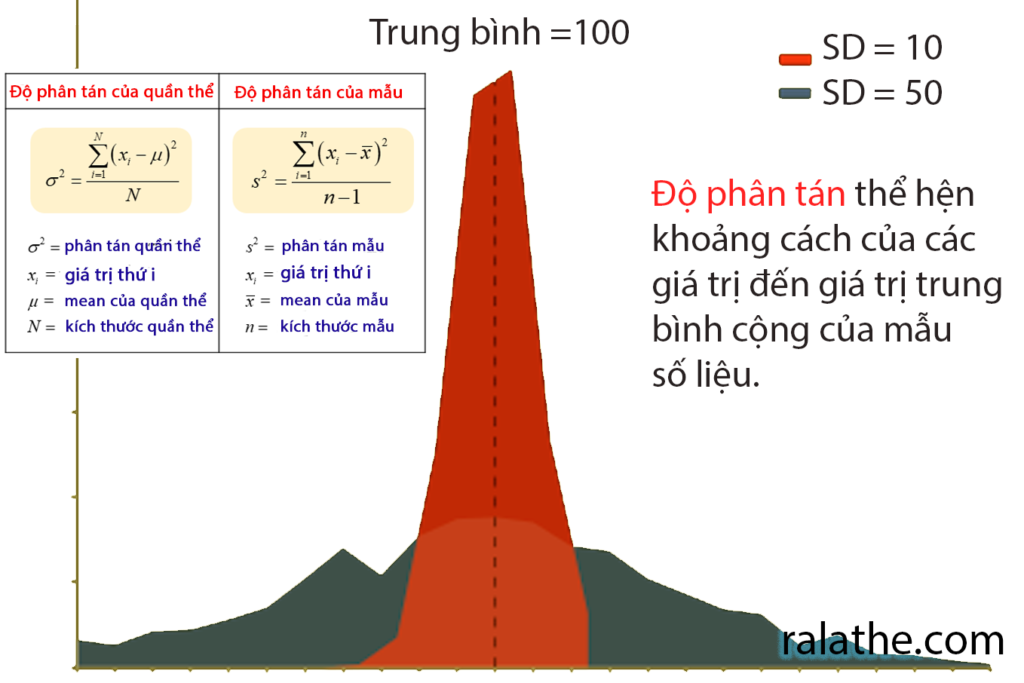
Vì thế, độ phân tán của các giá trị trong một mẫu tất nhiên sẽ nhỏ hơn so với độ phân tán của quần thể. Cho nên, để có thể ước lượng một cách chính xác độ phân tán của dữ liệu của quần thể, trong công thức tính độ phân tán ở trên, thay vì chia cho n, chúng ta sẽ chia cho n-1 để có được độ phân tán gần đúng hơn so với độ phân tán của quần thể.
[math]s^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (x_i – \bar{x})^2[/math]
>>>> Có thể bạn muốn biết: Ánh sáng xanh thực tế không làm bạn mất ngủ
Trong python, nếu ta tính độ phân tán bằng thư viện numpy thì sẽ là độ phân tán của chỉ mẫu số liệu của chúng ta (1/n):
import numpy as np
sample = [1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2]
print(np.var(sample))
print(np.std(sample))
###(kết quả trả về)###
6.358024691358025 # phương sai
2.521512381757826 # độ lệch chuẩnCòn nếu chúng ta dùng thư viện pandas hoặc scipy.stats, độ phân tán sẽ được tính là 1/(n+1):
from scipy import stats
import numpy as np
sample = [1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2]
print(stats.tvar(sample))
print(stats.tstd(sample))
###(kết quả trả về)###
6.732026143790851 # phương sai
2.594614835344709 # độ lệch chuẩn
Trong R, độ phân tán sẽ được tính là:
sample = c(1, 1, 2, 5, 2, 3, 9, 4, 6, 6, 4, 7, 5, 3, 8, 9, 3, 2)
var(sample)
sd(sample)
###(kết quả trả về)###
[1] 6.732026 # Phương sai
[1] 2.594615 # Độ lệch chuẩnNhư vậy, chúng ta có thể thấy là R cũng sẽ tính độ phân tán theo độ phân tán bất thiên (1/(n+1)).
Video bài số 3 của series thống kê cho khoa học dữ liệu
Bài giảng trong video này đến phút thứ 13:46 là hết bài 3.1 nhé!
>>>> Xem thêm: Cách hay nhất để bạn có thể dậy sớm (hoặc không)
