Trong bài 2 của loạt bài thống kê cho khoa học dữ liệu này, chúng ta sẽ cùng nhau tìm hiểu về biến ngẫu nhiên và tính trung tâm của giá trị đại diện cho dữ liệu, hay còn gọi là central tendency. Bắt đầu nhé!
Mục lục bài viết
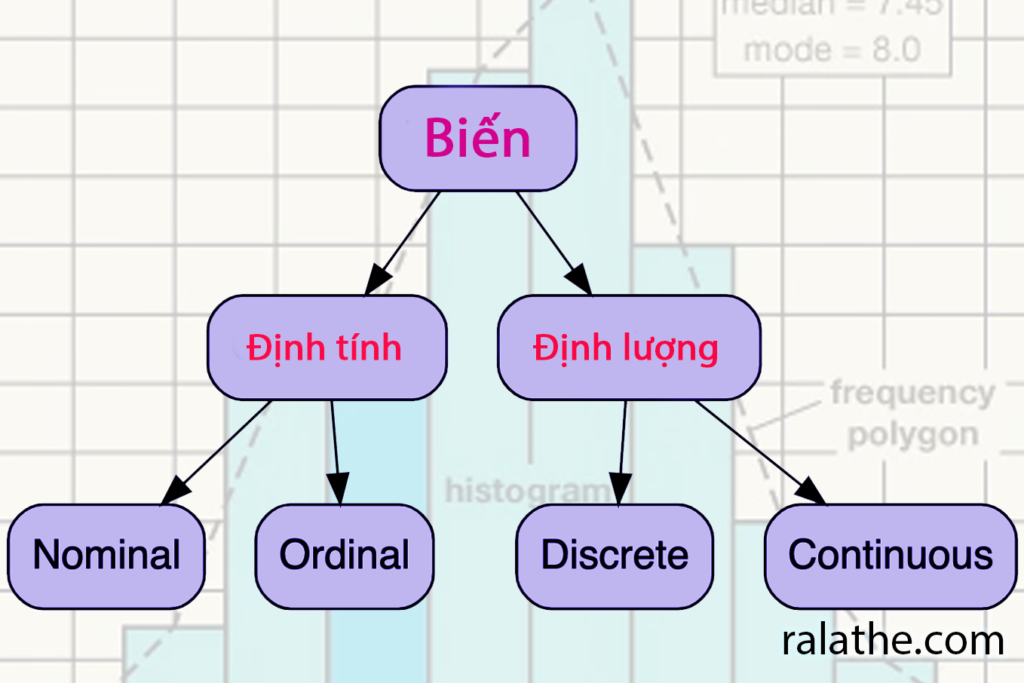
Biến ngẫu nhiên trong thống kê cho khoa học dữ liệu
Biến ngẫu nhiên là biến có giá trị không biết (ngẫu nhiên) hoặc là một hàm được gán cho giá trị ngẫu nhiên. Biến ngẫu nhiên có thể được phân ra thành biến định tính (qualitative variable hay categorical variable) và biến định lượng (quantitative variable).
Biến định tính
Biến định tính trong thống kê có thể được hiểu là biến không phải là số. Những biến này được sắp xếp vào các tập phân loại khác nhau. Chẳng hạn như nam, nữ; ngày, đêm; bàn, ghế, sách, bút; màu sắc (đỏ, xanh, vàng, cam, tím) v.v.
Biến định tính cơ bản có thể được chia thành biến có thể xếp hạng (ordinal) và không thể xếp hạng (nominal).
Biến nominal
Biến nominal là những biến không thể được xếp hạng hay sắp xếp. Ví dụ như bạn không thể nói nam lớn hơn nữ hay nữ lớn hơn nam được. Cũng như màu sắc, bạn không thể nói được màu đỏ lớn hơn hay nhỏ hơn màu vàng, xanh. Tất cả những biến như thế trong thống kê cho khoa học dữ liệu nói riêng và thống kê nói chung đều được gọi là biến định tính không thể xếp hạng hay biến nominal.
Biến ordinal
Ngược lại với biến nominal là biến ordinal, biến có thể được xếp hạng trong tập dữ liệu. Ví dụ như: nhóm tuổi từ 0-10, 10-20, 20-30, 30-40, …; hoặc là xếp hạng mức độ yêu thích của bạn với một sản phẩm nào đó từ 0 (không thích) đến 5 (rất thích).
Biến định lượng
Biến định lượng là biến có thể đo lường cũng như dùng số liệu để thể hiện ra được. Nói về biến định lượng thì nhiều vô số, chẳng hạn như thời gian, giờ, phút, giây; nhiệt độ; số tuổi – ở đây cần lưu ý là số tuổi khi nhóm thành từng nhóm tuổi thì lại là biến định tính – hay chiều cao, cân nặng. Tất cả những gì có thể dùng số để biểu diễn được.
Giống như biến định tính, biến định lượng cũng được chia ra thành hai loại là discrete (không có dấu thập phân) và liên tục.
Biến discrete (số nguyên)
Như tên gọi, trong thống kê cho khoa học dữ liệu, thì biến discrete là biến chỉ được thể hiện bằng số nguyên. Chẳng hạn như số con trong một gia đình, số người sinh sống, số ngón tay trên một bàn tay v.v. Những dữ liệu này không thể có số lẽ như 1.5 người (!?)
Biến liên tục (continuous)
Khác với biến discrete thì biến liên tục lại có thể được thể hiện bằng số thực, chẳng hạn như nhiệt độ, cân nặng, chiều cao v.v. Giá trị của biến này gồm tất cả những số thuộc tập số thực R.
Giá trị đại diện cho dữ liệu
Giá trị đại diện là giá trị có thể dùng để thể hiện tính chất của toàn bộ dữ liệu. Chẳng hạn như bạn đi câu cá, bắt được 10 con cá, khi được hỏi mỗi con nặng bao nhiêu ký thì bạn thường sẽ trả lời rằng mỗi con nặng trung bình khoảng 1kg. Ở đây, 1kg chính là giá trị đại diện cho toàn bộ giá trị của khối lượng từng con cá mà bạn câu được. Tất nhiên, cân nặng của mỗi con sẽ khác nhau, nhưng sẽ dao động xung quanh giá trị 1kg này. Nên 1kg có thể dùng làm giá trị đại diện cho cân nặng của số cá của bạn (có vẻ như bạn được một buổi đi câu bội thu nhỉ)
Thường giá trị đại diện sẽ gồm một trong ba giá trị (hoặc cả ba) là: trung bình (mean), trung vị (median), và yếu vị (mode)
Số trung bình
Có nhiều cách tính giá trị trung bình, hay thấy nhất là trung bình số học, trung bình điều hòa (nghịch đảo của trung bình nghịch đảo), và tỷ suất trung bình (trung bình hình học)
Trung bình số học
Khi làm thống kê cho khoa học dữ liệu hay data science, có lẽ các bạn sẽ quen với cách tính giá trị trung bình này nhất. Trung bình số học thường được tính theo công thức sau (với x là phần tử trong tập n giá trị):
[math]\bar{x} = \frac{x_1 + x_2 + x_3 + … + x_n}{n}[/math]
Nếu dùng python để tính thì code sẽ như thế này:
>>> import numpy as np
>>> soKyCuaCa = [0.9, 0.8, 1.1, 1.2, 1, 0.7, 1.3, 1.5, 0.6, 1.1]
>>> np.mean(soKyCuaCa)
1.02
Nếu dùng R thì code sẽ là:
> soKyCuaCa = c(0.9, 0.8, 1.1, 1.2, 1, 0.7, 1.3, 1.5, 0.6, 1.1)
> mean(soKyCuaCa)
[1] 1.02Tính chất quan trọng của trung bình số học
Trong thống kê cho khoa học dữ liệu nói riêng và thống kê nói chung, trung bình số học có hai tính chất quan trọng sau:
1. Tổng độ lệch (độ sai khác) từ các điểm dữ liệu đến giá trị trung bình cộng bằng 0.
Điều này có thể dễ dàng thấy được vì giá trị trung bình cộng nằm chính giữa của dữ liệu cách đều tất cả các điểm, nên khi tính độ lệch tổng cộng thì sẽ bằng 0 (đối xứng qua điểm trung bình cộng). Do tổng độ lệch bằng 0 nên ta sẽ có thể suy ra được tính chất thứ hai, đó là:
2. Tổng bình phương tất cả độ lệch từ các điểm dữ liệu đến giá trị trung bình cộng là nhỏ nhất.
Trung bình hình học (tỷ suất trung bình)
Giả sử bạn đi làm cho một công ty và theo quy định, thì lương của bạn sẽ được tăng so với năm trước là:
- Sau một năm tăng thêm 5%
- Sau hai năm tăng thêm 10%
- Sau ba năm tăng thêm 30%
Giả sử khi mới đi làm thì lương của bạn là 1000 $. Vậy sau ba năm lương của bạn sẽ là:
[math]1000(1+0.05)(1+0.10)(1+0.30) = 1501.5$[/math]
Vậy thì trung bình mức tăng lương hàng năm của bạn là bao nhiêu?
Nếu ta chỉ tính đơn thuần bằng công thức trung bình số học ở trên thì trung bình mỗi năm lương bạn sẽ tăng lên là:
[math]\frac{5\% + 10\% + 30\%}{3} = 15\%[/math]
Như vậy có đúng không? Hãy giành thời gian suy nghĩ chút nhé!
Nếu trung bình hàng năm tăng lên 10%, thì sau ba năm lương của bạn sẽ là:
[math]1000(1+0.15)(1+0.15)(1+0.15) = 1520.875$[/math]
Bạn thấy kết quả này so với kết quả thực tế khác rất nhiều. Do đó, để hạn chế sai khác, người ta có một cách tính khác, đó chính là tính theo tỷ suất. Công thức này được tính như sau:
[math]\bar{x} = \sqrt[n]{x_1x_2x_3…x_n}[/math]
Vậy nếu áp dụng công thức tỷ suất ở trên, thì trung bình mỗi năm lương sẽ tăng thêm là:
[math]\bar{x} = \sqrt[3]{1.05\times1.10\times1.30} = 1.1451[/math]
Và lương của bạn sau ba năm sẽ là:
[math]1000\times1.1451^3 = 1501.517$[/math]
Bạn có thể thấy giá trị này xác với giá trị thực tế hơn rất nhiều so với khi dùng trung bình cộng. Do đó, trong việc tính toán tăng theo tỷ suất trong thống kê cho khoa học dữ liệu, người ta thường dùng tới trung bình hình học (geometric mean) hơn là trung bình số học.
Code để tính trung bình hình học trong python sẽ là:
>>> from scipy import stats
>>> tySuatTangLuong = [1.05, 1.10, 1.30]
>>> tySuatTangLuongTB = stats.gmean(tySuatTangLuong)
>>> print(tySuatTangLuongTB)
1.1450956868476592Còn trong R sẽ là:
> tySuatTangLuong = c(1.05, 1.10, 1.30)
> exp(mean(log(tySuatTangLuong)))
[1] 1.145096>>>> Xem thêm: Nhìn chó biết mặt chủ. Vì sao cả hai đều như nhau
Trung bình điều hòa
Trung bình điều hòa hay là harmonic mean, hay là nghịch đảo của trung bình nghịch đảo. Công thức của cách tính này như sau:
[math]\bar{x} = \frac{1}{\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+…+\frac{1}{x_n})}[/math]
Chúng ta thường bắt gặp cách tính trung bình này trong vật lý, khi tính vận tốc trung bình của cả quãng đường đi được. Ví dụ như: Quãng đường AB có độ dài là d = 60 km, nếu bạn đi từ A đến B với vận tốc [math]x_1 = 20 km/h[/math] và đi ngược lại từ B đến A với vận tốc là [math]x_2 = 60 km/h[/math]. Vậy vận tốc trung bình của bạn có phải là [math]\frac{x_1+x_2}{2} = 40 km/h[/math] không?
Nghe có vẻ hợp lý! Bây giờ thử tính lại bài toán này theo thời gian thì sao nhỉ?
Thời gian đi từ A đến B sẽ là
[math]t_1 = \frac{d}{x_1} = \frac{60}{20} = 3 h[/math]
Thời gian đi từ B đến A sẽ là
[math]t_2 = \frac{d}{x_2} = \frac{60}{60} = 1 h[/math]
Tổng thời gian sẽ là 3 + 1 = 4 h. Vậy Vận tốc khi đi hết cả quảng đường A-B-A sẽ là:
[math]\frac{2d}{t_1+t_2} = \frac{2\times60}{4} = 30 km/h[/math]
Rõ ràng, tính vận tốc trung bình bằng công thức này sẽ hợp lý hơn, đúng không nào!
Code để tính trung bình hình học trong python sẽ là:
>>> from scipy import stats
>>> vanToc = [20,60]
>>> vanTocTB = stats.hmean(vanToc)
>>> print(vanTocTB)
30.0Code trong R sẽ là:
> library("psych")
> vanToc = c(20,60)
> print(harmonic.mean(vanToc))
[1] 30Video bài giảng số 2 của thống kê cho khoa học dữ liệu
Để có thể hiểu rõ hơn, hãy cùng nhau tìm hiểu qua video bài giảng này nhé!
